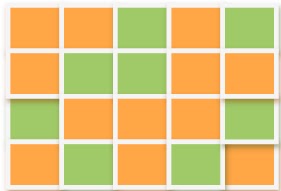
No se sabe donde están los números,
pero el sabueso es capaz de encontrarlos. Las casillas verdes contienen números
primos: 2, 3, 5,7, 11, 12, 13, 17 y 19. Con estos datos, ¿Qué camino seguirá
el sabueso? o ¿Dónde se encuentra oculto cada número del 1
al 20?
Influencia y aplicacion de las Matemáticas en la Vida cotidiana. Las Matemáticas nos ayudan a profundizar en la percepción del mundo, buscando el control racional del espacio físico, las situaciones problemáticas, los fenómenos naturales y sociales. En este espacio podrás encontrar información que te sera útil para comprender las matemáticas y su comportamiento en el marco urbano.
miércoles, 18 de julio de 2012
Sabuesos De Primos
Un sabueso de primos es capaz de seguir de
seguir la secuencia de los números naturales ocultos en un tablero: comienza en
la casilla marcada con 1, pasa a la 2, luego a la 3, y continúa así hasta
llegar a la 20. El sabueso avanza de casilla en casilla, en el horizontal o en
vertical, nunca en diagonal. Cada casilla es visitada una sola vez.
Recta Larga
A lo largo
de una carrera se encuentran ubicados 5 pueblos: Tamino, Pamino, Balda, Calda y
Malda. Cada población tiene un único cartel, que señala hacia una de las otras
cuatro: los carteles, aunque no están necesariamente en orden, tiene las siguientes
inscripciones:
Solo uno de los cuatro carteles tiene marcada la dirección. Se pide
colocar las fechas a los otro cuatro carteles.
Problema De Teano
Cuenta la
leyenda que un discípulo de Pitágoras le consulto sobre la edad de la bella
Teano. Pitágoras le respondió:
Teano es
perfecta, y su edad es un número perfecto.
¿Podría
darme más información? – pidió el joven.
La edad de
Teano – dijo Pitágoras – es el número de sus extremidades, multiplicado por el
número de sus admiradores, que es un número primo.
Sabiendo
que los números perfectos son aquellos que son iguales a la suma de sus
divisores propios,
¿Cuál es la edad de Teano, y cuantos admiradores tenia?
Los Huevos Rotos
Una anciana camina con una canasta de huevos en
el brazo. Un caballo la asusta y, al caer, todos los huevos se rompen. Con la
intención de pagárselos, el jinete pregunta a la mujer, cuantos huevos llevaba
en la canasta. La mujer dice recordar que, ordenados en paquetes de dos, tres.
Cuatro y cinco huevos, le sobran 1, 2, 3 y 4 huevos, respectivamente.
¿Cuál es
el mínimo número de huevos que había en la canasta?
La Parabola, La Elipse Y La Hiperbola
Los antiguos griegos profundizaron en el
estudio de las secciones cónicas y descubrieron propiedades que permitían
definir tales curvas en términos de puntos y rectas. Actualmente las cónicas
son un medio importante para las investigaciones en el espacio exterior y para
el análisis del comportamiento de las partículas atómicas.
Las secciones cónicas son curvas que pueden
obtenerse de la intersección de un plano con un cono circular recto. La
intersección de un cono con un plano perpendicular a su eje produce una
circunferencia. Si el plano se inclina ligeramente, la curva resultante es una
elipse. Cuando el plano es paralelo a una recta sobre el cono, la curva de la
intersección es una parábola. Finalmente, si el plano interseca ambas mitades,
o ramas del cono, la curva es una parábola. Estas cuatro secciones cónicas
básicas se ilustran en la figura anterior.
Granjero Obsesivo
Un granjero tiene 36 gallinas. Por alguna
razón, ha construido un gallinero con jaulas distribuidas como muestra la
figura:
Coloca en cada jaula una cantidad diferente de
gallinas: en una jaula, 1 gallina, en otra, dos gallinas; en la tercera, 3, y
sigue así hasta ubicar en la octava
jaula 8 gallinas. Pero lo más curioso de su obsesión es lo siguiente: en
ningún caso dos jaulas vecinas (ni contiguas por un lado, ni diagonal) contiene
cantidades consecutivas de gallinas. Es decir, si una jaula contiene, por
ejemplo 5 gallinas, en las vecinas no puede haber ni cuatro ni seis. ¿ de qué
modo distribuye el granjero sus gallinas?
Foto De Familia
Se quiere
sacar una foto familiar de seis personas, de las que todas tienen estaturas
diferentes. El fotógrafo quiere ordenarlas en dos filas de tres, ambas con
alturas crecientes de izquierda a
derecha, y de modo que cada persona de la fila de atrás sea más alta que la que
tiene adelante.
¿De cuantas
formas diferentes puede hacerlo?
El Tamaño Del Universo
Hasta hace poco se creía que las dimensiones de
la tierra eran inmensas. Hace algo más de cuatro siglos le llevo a Fernando
Magallanes y sus hombres casi tres años circunnavegar el globo terrestre.
· Haz un listado con las palabras cuyo significado desconoces y búscalo en el diccionario.
· En un máximo de 10 renglones realiza un resumen de las ideas fundamentales expresadas en la lectura.
· Con el siguiente dato puedes traducir todas las distancias dadas a escala en la lectura, a su dimensión real: un metro se define como “la diezmillonésima parte del cuadrante del meridiano terrestre”; como es lógico, la circunferencia de la tierra tiene cuatro cuadrantes.
En 1961, nuestros primeros viajeros al espacio,
Garin y Titov, dieron la vuelta al globo en 89 minutos en la nave cósmica
“Vostok”. Así, a medida que se han ido construyendo vehículos más veloces, se
ha encogido el tamaño aparente de la tierra.
En nuestro sistema solar son 9 los planetas
conocidos. La tierra está situada relativamente cerca del sol, aunque mercurio
y Venus están más próximos. La distancia media del sol a su planeta más remoto,
Plutón, es cuarenta veces mayor que la existente entre el sol y la tierra.
El diámetro del sistema solar es
aproximadamente de 50 a 100 unidades astronómicas, anos 10 mil millones de
kilómetros. En nuestra escala de distancias, es una cifra muy grande, como un
millón de veces mayor que el diámetro de la tierra.
Podemos percatarnos mejor de los tamaños
relativo de nuestro sistema solar si imaginamos un modelo a escala. Hagamos que
el sol este representado por una bola de billar de 7 cm de diámetro; con esta
escala mercurio, el planeta más próximo al sol, estaría a una distancia de 280
cm, la tierra a 760 cm, Júpiter el más grande de los planetas, casi a 300 m de
la bola de billar. El diámetro de la tierra tendría un poco mas de 0,7 mm; el
de la luna seria aproximadamente 0,1 mm y el de su órbita alrededor de la tierra,
4 cm. La estrella más próxima después del sol, Alfa Centauro, habría que
colocarla a 2000 km, distancia tan remota que, por comparación, haría aparecer
insignificantes las inmensas distancias planetarias a escala.
El kilometro, el centímetro, la milla y las
demás unidades de medida, se adoptaron por necesidades prácticas del hombre en
la tierra, pero resulta evidente que no son apropiadas para calibrar las
distancias cósmicas. En ciencia ficción y a veces en obras científicas se
emplea el “año luz” para medir las distancias interestelares e intergalácticas.
Un año luz es la distancia que recorre la luz en un año a la velocidad de
300.000 km por segundo.
COMPRENSION
DE LECTURA:
· Haz un listado con las palabras cuyo significado desconoces y búscalo en el diccionario.
· En un máximo de 10 renglones realiza un resumen de las ideas fundamentales expresadas en la lectura.
· Con el siguiente dato puedes traducir todas las distancias dadas a escala en la lectura, a su dimensión real: un metro se define como “la diezmillonésima parte del cuadrante del meridiano terrestre”; como es lógico, la circunferencia de la tierra tiene cuatro cuadrantes.
a. ¿Cuál es la longitud en metros de un
cuadrante del meridiano terrestre?
b. ¿Cuál es, en metros, la longitud de
la circunferencia?
c. ¿Cuál es el radio de la tierra?
d. Escribe el radio de la tierra en
notación científica.
e. El radio del sol es aproximadamente
100 veces el radio de la tierra. Calcule el radio del sol.
f. Como en el modelo, el sol se
representa con una bola de billar de 7 cm de diámetro; calculen en realidad a
cuanto equivale un centímetro de la escala.
1.
Teniendo
en cuenta que la luz viaja a una velocidad de 300.000 km por segundo, calculen
el tiempo que tarda la luz en llegar hasta cada uno de los planetas.
2.
Si
se emite una señal luminosa desde la tierra, ¿Qué tiempo tarda en llegar la luz
a la luna?
3.
Si
se produjera una explosión en el sol, ¿Cuánto tiempo después nos daríamos
cuenta de ello?
El numero π
Seguro que sabes que el numero π se utiliza
habitualmente en matemáticas para llevar a cabo cálculos geométricos como la
longitud de una circunferencia o el área de un circulo, entre otros. Lo que
quizás no sepas es que este famoso numero es conocido desde la antigüedad, pues
ya en el año 1650 a.c. aparecen referencias en Egipto en las que se le asigna
el valor de 3, 16.

En el siglo III a.c., el gran Arquímedes de
Siracusa, físico, matemático e inventor de la Grecia clásica, se ocupo también
de él y estableció que π estaba comprendido entre 22/7 y 221/71; esta
aproximación del valor de π se utilizo hasta la edad media, y es en el siglo
XV, en la India, cuando se usa por primera vez una serie infinita convergente
para su cálculo más exacto.
Por cierto, que el numero en cuestión no tuvo
ningún nombre en particular durante varios siglos. Designarlo con la letra
griega π (pi) fue idea del ingles William Jones, en 1706. Se trata de acuerdo
con nuestra clasificación actual, de in numero irracional (decimal no periódico), que cuenta con un
número ilimitado de cifras decimales. Esto ya se sabía desde la antigüedad y,
en consecuencia, no es de extrañar que se hayan dedicado innumerables esfuerzos
a tratar de conocer con mayor exactitud su valor.

Entre los matemáticos que se han dejado seducir
por π, se destacan el francés Franciscus Vieta, que le calculo, en el siglo
XVI, 10 cifras decimales y el alemán Ludolph Van Ceulen, que murió en 1610 y
pidió que se grabaran en su lapida las 35 cifras decimales que había calculado.
Sin embargo, esto no es nada comparado con lo que sucedió a mediados del siglo
XX.
La llegada de los ordenadores marco un antes y
un después del cálculo de π; el ENIAC, trabajando durante 70 horas, determino
2037 cifras decimales exactas en 1949. La progresión continuo imparable a
medida que se perfeccionaban los equipos. Por ejemplo, en 1999 los japoneses
Kanada y Takahashi obtuvieron con ayuda de un ordenador Hitachi SR8000 más de
68.000 millones de cifras decimales. Diez años después, en 2009, el record ha
sido pulverizado. Takahashi ha logrado más de dos billones y medio de cifras.
Su secreto: una supercomputadora T2K Tsukuba System, formada por 640
computadoras de alto rendimiento conectadas, funcionando durante 73 horas y media.
¿Quién da más?
Curiosidades sobre el número Pi
Pi es la razón de la circunferencia de un círculo a su diámetro. En
distintas culturas, china, egipcia, europea, india, etc., se trato de obtener
mejores aproximaciones de Pi por ser de aplicación en campos tan distintos como
la astronomía o la construcción. A continuación les exponemos algunas de las
curiosidades sobre este peculiar número.
- Muchos
de los intentos de evaluar Pi en la antigüedad utilizaban el método de
calcular el perímetro de polígonos inscritos y circunscritos a
circunferencias.
- Modernamente
para evaluar Pi se utiliza una serie infinita convergente. Este método fue
utilizado por primera vez en Kerala (India) en el Siglo XV
- La
probabilidad de que dos enteros positivos escogidos al azar sean primos
entre si es 6/Pi2
- Si se
eligen al azar dos números positivos menores que 1, la probabilidad de que
junto con el número 1 puedan ser los lados de un triángulo obtusángulo es
(Pi-2)/4
- En
1706, el inglés William Jones fue el primero en utilizar el símbolo
griego para denotar la relación entre
la circunferencia y su diámetro. Euler en su obra
"Introducción al cálculo infinitesimal", publicada en 1748, le
dio el espaldarazo definitivo.
- Muchos
intentos para determinar Pi con exactitud están relacionados con el
clásico problema de la cuadratura del círculo : "construir,
utilizando únicamente regla y compás, un cuadrado de área igual a un
círculo dado".
- Johan
Heinrich Lambert(1728-1777), matemático alemán, probó que Pi es irracional. ( Un
número irracional no se puede escribir en forma de fracción racional.
Números racionales son : 1, 2 , 3/4, 17/23)
- El
matemático alemán Ludolph van Ceulen(1540-1610) pidió que, como
epitafio, escribiesen en su lápida las 35 cifras del número Pi que había
calculado. Los alemanes llaman a Pi el número ludofiano.
- William
Shanks,
matemático inglés, dedico 20 años de su vida a la obtención de 707
decimales de Pi.(En 1945 se descubrió que había cometido un error en el
decimal 528 y a partir de este todos los demás eran incorrectos)
- En 1949
uno de los primeros ordenadores el ENIAC, trabajando durante 70
horas, determino Pi con 2037 decimales.
- En
1959, ordenadores en Francia e Inglaterra calcularon más de 10.000 cifras
de Pi.
- En 1961
Daniell Shanks(sin relación con William Shanks) y Wrench,
obtuvieron en 8 h 23 min, 100.265 cifras en un IBM 7090.
- En
1983, Yoshiaki Tamura y Yasumasa Kanada, en menos de 30 h,
en un HITAC M-280 H obtuvieron 16.777.206 (224) cifras.
- En Julio de 1997, Yasumasa Kanada y Daisuke Takahashi obtuvieron 51.539.600.000 cifras , utilizando un HITACHI SR2201 con 1024 procesadores.
Conceptos elementales de probabilidad
La mayoría de las personas tiene una noción intuitiva
de lo que se entiende por probabilidad, aunque no pueda dar una definición.
Casi todos hemos tenido experiencias relacionadas con
incertidumbre asociadas a las condiciones del tiempo o a juegos de azar. Además
la palabra probabilidad está relacionada con otras como: posibilidad,
eventualidad, las cuales son utilizadas con mucha frecuencia en la vida diaria
alrededor de hechos cuya verificación es incierta.
Por ejemplo, se suele decir "es probable que
llueva esta tarde", dando a entender que se tiene mucha confianza o
seguridad de que el evento "llueva esta tarde" sí suceda.
La probabilidad es, en realidad, un valor numérico que
debe cumplir con ciertas condiciones o propiedades matemáticas y que se asocia
a un evento o suceso determinado para expresar el grado de confianza en la
verificación futura de dicho evento.
Así, por ejemplo, ocurre con las noticias sobre el
pronóstico del tiempo, los funcionarios que comunican en la televisora tienen
un grado de confianza en su pronóstico, con base en los datos recogidos por
medio de observaciones, registros y procesos repetitivos.
Evento o Suceso
Un evento es un conjunto formado por uno o más
posibles resultados, asociados a un experimento aleatorio, por ejemplo al
lanzar un dado numerado de 1 al 6, los eventos serían: 1, 2, 3, 4, 5, 6.
Tipos de Eventos:
Existen eventos imposibles, improbables, probables,
seguros:
- Es probable que me bañe.
- Es seguro que amanezca después de la noche.
- Es imposible que mañana sea domingo, si hoy es lunes.
- Es improbable que mamá me deje sin desayunar.
- Cuando llueve la tierra se moja (esto es seguro).
- Mi tía encuentra una olla llena de monedas de oro (esto es posible, pero no probable).
- Juan juega en el patio con sus compañeros, él no está solo en el patio (esto es probable).
¿Puede clasificar los eventos anteriores?
Si hacemos observaciones y representaciones acerca de
las diversas actividades que realizamos o sobre eventos naturales que ocurren
diariamente, se pueden clasificar y ordenar según su probabilidad de
ocurrencia.
Los conceptos "seguro",
"imposible" o "casual"
- Seguro: lo que siempre ocurre.
- Imposible: lo que nunca sucede (ni sucederá).
- Casual: lo que puede suceder.
Cajas Autoreferentes
La caja del
dibujo tiene cuatro ventanas, en cada una de las cuales hay que colocar un
digito repetido o no.
Al terminar se habrá formado un número de cuatro dígitos. Se pide que el digito colocado en cada ventana indique la cantidad de veces que la cifra que esta sobre dicha ventana aparece en el numero formado: si, por ejemplo, en la ventana bajo cero se coloca el 2, significa que ha de haber dos ceros en el numero formado al final.
Al terminar se habrá formado un número de cuatro dígitos. Se pide que el digito colocado en cada ventana indique la cantidad de veces que la cifra que esta sobre dicha ventana aparece en el numero formado: si, por ejemplo, en la ventana bajo cero se coloca el 2, significa que ha de haber dos ceros en el numero formado al final.
Una vez resuelto el caso anterior, probar con
esta otra caja, siguiendo las mismas normas:
Amor Entre Las Fracciones
Mi protagonista se llama 1/4, ella es mayor de
edad y quiere casarse y tener hijos; su
marido debe ser equivalente a ella, por ejemplo ella puede casarse con 2/8,
3/12, 4/16… Cierto
día 1/4 decidió salir a dar una vuelta con su amiga 1/5, se fueron a
cenar y después a bailar a una discoteca.
Como era normal, 1/5, salió a bailar y se hizo
amiga de una fracción que no era equivalente a ella, pero le daba igual, porque
al día siguiente ni la recordaría, como solía decir “esto es un rollito de un
día”.
1/4 se
fue a la barra para tomar un refresco, estaba muy aburrida y apunto de
dormirse, entonces miro el reloj y vio que era muy tarde, fue entonces a buscar
a 1/5 a la pista de baile para irse a casa; en ese momento sin querer una
fracción que pasaba por allí le derramo el refresco sobre su vestido, 1/4 se
enfado mucho, porque era su vestido favorito, además se trataba de un chico y
le pareció algo vulgar, este apenado le
dijo que lo disculpara… que además le pagaría el traje; 1/4 le dijo de manera descortés ¡tranquilo,
no hace falta!. Tanta fue la insistencia
del chico, que entablaron una amena conversación; a estas alturas ya nuestra
protagonista sin tener conciencia de ello, se había enamorado; el chico entre
muchas otras cosas, le dijo que se llamaba 2/8 y que estaba esperando una
fracción equivalente para casarse y formar una familia. Que grata casualidad
ambos estaban buscando lo mismo…
En ese momento llego 1/5 a recordarle que ya
era demasiado tarde, el chico, las acompaño hasta su casa; acordaron de seguir
hablando el día siguiente para conocerse mejor.
Esa noche, 1/4, tuvo un fantástico sueño en el
que se casaba con 2/8. ¡Deseaba hacer realidad ese sueño!
De repente sonó el
teléfono, escucho la voz que anhelaba, la de 2/8, que la invito a dar una
vuelta; ella se arreglo apresuradamente, 2/8 paso a recogerla en un hermoso
auto deportivo, visitaron muchos lugares, hablaron de sus sueños e ilusiones, y
así pasaron varios días; cada día resultaba corto para compartir y su relación
se hacía más fuerte. Les iba también juntos que decidieron casarse.

La ceremonia no fue religiosa porque en el mundo de las matemáticas no se entiende de religión.
Se fueron de luna de miel a un cuaderno de matemáticas de un estudiante de 7° grado. Allí la pasaron muy bien porque había muchas fracciones, lugares y situaciones divertidas.
Tuvieron una hija hace algunos meses a la que
llamaron 1/2, porque:
1/4 + 2/8 = 1/2 ya que 4/16 + 4/16 = 8/16 8/16 = 1/2
Suscribirse a:
Comentarios (Atom)