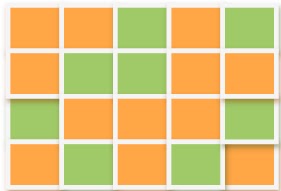
No se sabe donde están los números,
pero el sabueso es capaz de encontrarlos. Las casillas verdes contienen números
primos: 2, 3, 5,7, 11, 12, 13, 17 y 19. Con estos datos, ¿Qué camino seguirá
el sabueso? o ¿Dónde se encuentra oculto cada número del 1
al 20?
Vive Y Construye Las Matemáticas
Influencia y aplicacion de las Matemáticas en la Vida cotidiana. Las Matemáticas nos ayudan a profundizar en la percepción del mundo, buscando el control racional del espacio físico, las situaciones problemáticas, los fenómenos naturales y sociales. En este espacio podrás encontrar información que te sera útil para comprender las matemáticas y su comportamiento en el marco urbano.
miércoles, 18 de julio de 2012
Sabuesos De Primos
Un sabueso de primos es capaz de seguir de
seguir la secuencia de los números naturales ocultos en un tablero: comienza en
la casilla marcada con 1, pasa a la 2, luego a la 3, y continúa así hasta
llegar a la 20. El sabueso avanza de casilla en casilla, en el horizontal o en
vertical, nunca en diagonal. Cada casilla es visitada una sola vez.
Recta Larga
A lo largo
de una carrera se encuentran ubicados 5 pueblos: Tamino, Pamino, Balda, Calda y
Malda. Cada población tiene un único cartel, que señala hacia una de las otras
cuatro: los carteles, aunque no están necesariamente en orden, tiene las siguientes
inscripciones:
Solo uno de los cuatro carteles tiene marcada la dirección. Se pide
colocar las fechas a los otro cuatro carteles.
Problema De Teano
Cuenta la
leyenda que un discípulo de Pitágoras le consulto sobre la edad de la bella
Teano. Pitágoras le respondió:
Teano es
perfecta, y su edad es un número perfecto.
¿Podría
darme más información? – pidió el joven.
La edad de
Teano – dijo Pitágoras – es el número de sus extremidades, multiplicado por el
número de sus admiradores, que es un número primo.
Sabiendo
que los números perfectos son aquellos que son iguales a la suma de sus
divisores propios,
¿Cuál es la edad de Teano, y cuantos admiradores tenia?
Los Huevos Rotos
Una anciana camina con una canasta de huevos en
el brazo. Un caballo la asusta y, al caer, todos los huevos se rompen. Con la
intención de pagárselos, el jinete pregunta a la mujer, cuantos huevos llevaba
en la canasta. La mujer dice recordar que, ordenados en paquetes de dos, tres.
Cuatro y cinco huevos, le sobran 1, 2, 3 y 4 huevos, respectivamente.
¿Cuál es
el mínimo número de huevos que había en la canasta?
La Parabola, La Elipse Y La Hiperbola
Los antiguos griegos profundizaron en el
estudio de las secciones cónicas y descubrieron propiedades que permitían
definir tales curvas en términos de puntos y rectas. Actualmente las cónicas
son un medio importante para las investigaciones en el espacio exterior y para
el análisis del comportamiento de las partículas atómicas.
Las secciones cónicas son curvas que pueden
obtenerse de la intersección de un plano con un cono circular recto. La
intersección de un cono con un plano perpendicular a su eje produce una
circunferencia. Si el plano se inclina ligeramente, la curva resultante es una
elipse. Cuando el plano es paralelo a una recta sobre el cono, la curva de la
intersección es una parábola. Finalmente, si el plano interseca ambas mitades,
o ramas del cono, la curva es una parábola. Estas cuatro secciones cónicas
básicas se ilustran en la figura anterior.
Suscribirse a:
Comentarios (Atom)